à partir de trois éléments de la logique des prédicats du premier ordre et de la théorie des ensembles,
1. Condition à laquelle doit satisfaire une classe pour dire qu'elle est un ensemble.
L'énoncé qui permet d'établir ce fait : ∃x∀y((y ∈ x ) ⇔ P(y)) ..........p2
Cet énoncé écrit l'équivalence de deux modes distincts de relations à propos d'éléments notés ici : y
Les y satisfont à deux relations qui sont initialement différentes du fait de s'écrire différemment.
(y ∈ a), y appartient à a,
P(y), y satisfait la relation P, il fait partie de son extension, la classe qui s'écrit P(x).
- De la première relation, l'énoncé en question dit que l'autre élément,
l'ensemble noté a, existe ∃x R(x).
- Conclusion l'équivalence des deux relations permet d'écrire P(y) de manière plus directe (y ∈ a),
Dans ce cas la classe déterminée comme extention de la relation P(y) s'écrivant grâce à la relation appartenance comme l'appartenance à un ensemble a, cette classe est un ensemble.

Pour insister encore l'extension de P(y) équivaut à l'extension de (y ∈ a) qui se lit " y appartient à a ", et pourquoi ne pas dire que la classe, ou collection, des y est l'ensemble a.
De manière plus succinte : " la classe P(y) est un ensemble " puisque cette classe s'appelle a, elle est a. Il doit être évident pour le lecteur qu'il s'agit d'un jeu de mots dans la langue.

2. ............ Le schéma de compréhension,.....suite en haut droite,.................>

(suite), 2. Le schéma de compréhension. ................................................................p3
Formule du schéma : ∀x∃y(∀z((z ∈ y) ⇔ ((z ∈ x) ∧ P(z))).
Notons cet ensemble x donné : a et
cet autre ensemble y nécessaire : a'.
Nous parlerons de la trace de la classe P(z) sur l'ensemble a, pour désigner cette classe conjonction de la classe (z∈a) et de la classe P(z).

ce schéma écrit :
"Étant donnés un ensemble noté : x, et une classe P(z), quelconques tous les deux,
il existe un autre ensemble y, tel que tout les éléments z de a'
sont des éléments de l'ensembles a qui satisfont le prédicat P."

C'est la trace de la relation P(z) sur l'ensemble a qui est un ensemble a', donnant lieu à l'introduction de nouveau caractère afin d'écrire a' en fonction de a et de P puisqu'il se démontre (conditions requises) que cette fonction existe et qu'elle est fonctionnelle,

a'= {(z ∈ a) /P(z)}

voilà pour ce mathème hyper classique qu'un enfant ? de l'enseignement secondaire apprend à pratiquer intuitivement avec la notion qu'il y a de la raison dans cette manière d'écrire.
- Ce schéma est une conséquence du schéma d'axiome de substitution.

(plus sur le schéma d'axiome de substitution in :
Lecture des formules de la sexuation, 00, texte de 46 pages, *,
du 25 décembre 2007,
2.3. Le schéma d'axiome de substitution et son corrélat le schéma d'intention (ou de compréhension). p11
et "notre" Annexe n° 4, *, )

suite .... point 3, ci-dessous à gauche,

3. Les kantificateurs restreints ou énoncés restreints.

Ils sont définis par les deux énoncés suivants.

∀S xP(x) ∀x(S(x) ⇒ P(x))

∃S xP(x) ∃x(S(x) ∧ P(x))

I. 0.

Il existe une classe qui n'est pas un ensemble.

¬∃x∀y((y ∈ x) ⇔ (y y))

Reformulation pour démontrer ce fait ! ........................................................p3 & 4

I.0 - Dans une quelconque théorie des ensembles, il existe une classe qui n'est pas un ensemble (Russell).

Dans une quelconque théorie des ensembles il existe une classe qui n'est pas un ensemble de cette théorie.

La classe des ensembles qui ne s'appartiennent pas à eux mêmes ne peut pas être un ensemble (Russell) car si il existe un tel ensemble l'énoncé suivant est valide dans la théorie.

∃x∀y((y ∈ x) ⇔ (y y))

et nous pouvons introduire l'objet dont l'existence est ainsi assertée compte tenu de son unicité (axiome d'extensionalité). Notons le: a. Ainsi cet énoncé devient par instanciation de a à la place de x,

∀y((y ∈ a) ⇔ (y y))

Mais nous devons alors tenir compte aussi de ce que cet énoncé implique du
fait de son kanteur universel, soit que

((a ∈ a) ⇔ (a a))

conséquence invalide du fait de la contradiction qu'il représente puisqu'il écrit qu'une
proposition est équivalente à sa négation. ............................(suite) à droite, ........>

(suite),

Or le fait que l'énoncé

∃x∀y((y ∈ x) ⇔ (y y))

implique

((a ∈ a) ⇔ (a a))

suffit à établir qu'il est lui-même invalide.
Car la contraposition de

(∃x∀y((y ∈ x) ⇔ (y y))⇒((a ∈ a) ⇔ (a a)))

donnant

(¬((a ∈ a) ⇔ (a a))⇒ ¬∃x∀y((y ∈ x) ⇔ (y y)))

nous sommes assuré que la conséquence d'une tautologie est elle même
vraie de manière nécessaire, soit que

¬∃x∀y((y ∈ x) ⇔ (y y))

doit être une thèse de notre théorie.

Ainsi notre proposition est démontrée.

Dans une quelconque théorie des ensembles il existe une classe qui n'est pas un ensemble de cette théorie.

Ce que nous résumons par l'expression si elle est bien entendue comme il convient selon nos explications initiales : "Il existe une classe qui n'est pas un ensemble."

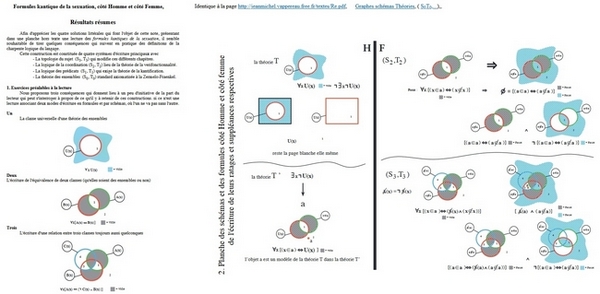
C.-Il n'échappera à personne que le premier argument
                                     1.∃x(C(x) ∧¬E(x))
c'est ce que nous avons établit dans ses raisons, dût à B. Russell, et à quel prix, lors de notre étape précédente :
                                   Il existe une classe qui n'est pas un ensemble.
                    D'où notre conclusion maintenant
                                        3. ¬E(u) .

La classe universelle U(x) d'une théorie des ensembles qui admet comme thèse ∀xU(x) , n'est pas un ensemble de cette théorie.

Par exemple nous pouvons considérer la théorie des ensembles finis qui admet comme axiome
∀xf(x) avec le prédicat f(x) : "x est fini" pour former cet axiome de cette théorie.

Ce que nous résumons par l'expression, si elle est bien entendue comme il convient :
"La classe universelle n'est pas un ensemble."

Nous avons ainsi proposé une lecture des formules de la sexuation écrite dans le cas où la classe universelle en question est la fonction phallique.
Si nous définissons la fonction Φ(x) : "x tombe sous la fonction imaginaire du phallus symbolique."
Les énoncés

∀xΦ(x)

∃x¬Φ(x)

sont susceptibles du même commentaire que celui que nous venons de développer pour une quelconque fonction dite universelle noté U(x) du fait que

∀xU(x)

et la théorie qui déduit les conséquences de cet axiome portant sur la fonction phallique, est susceptible d'être fondée par cette existence qui nie la fonction

∃x¬U(x)

donnant lieu à un objet a et à une réécriture de toute la théorie par des énoncés restreints à l'ensemble a en commençant par l'axiome universel qui peut être écrit comme

∀x((x ∈ a) ⇒ U(x)) .

sous l'aspect de

∀x((x ∈ a) ⇒ Φ(x))

dans le cas de la fonction phallique.

Noter que dans cette logique classique (Aristote), ce qui n'est pas P(x) est non P(x), d'où son universel machiste rabaissant le phallus symbolique sur le Phallus imaginaire confondu avec le Grand Pan, le dieu Pan, le dieu de la nature qui saurait lire.
Aristote, suivit par Kant, Goethe, Jung... et quelques autres qui sont légions aujourd'hui, manifeste par là, dans le traité de L'Âme et ceux qui lui sont attenant, la méconnaissance de la fonction paternelle traitée dans ce qui précède, côté Homme.
Aporie freudienne résolue par Lacan au travers d'une série d'indications et un trou dans son séminaire à cet endroit.
Maintenant nous pouvons passer au commentaire des formules côté femmes.

---------------------------------------------------------------

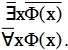
suite du texte, page 9, à gauche ci-dessous,

II. 0.
Modification de la logique elle même
deux négations supplémentaires ~ (x ∈ x) et
condition imposée à l'objet de B. Russell
∃x∀y(((y ∈ x) ⇔~ (y ∈ y)) ⇒ )

Nous modifions la logique elle même en introduisant un simple et unique caractère de négation supplémentaire qui nous permettra ici de formuler la condition à laquelle doit satisfaire un ensemble, si d'aventure il existait du fait d'être inscriptible grâce à cette logique, la négation de la relation d'appartenance cessant de ne pas s'écrire comme un ensemble. Soit la classe des ensembles qui ne s'appartiennent pas à eux mêmes.

Nous choisissons de substituer ici à la fonction phallique des formules afin de
développer notre commentaire à son propos,

c(x) : (x ∈ x)

paradigmatique de ce type de cas.
Nous avons déjà vu plus haut [I.0.] qu'en logique classique

¬∃x∀y((y ∈ x) ⇔ (y y)) .

Ici nous proposons de construire l'ensemble en question dans le cas de la négation de la relation d'appartenance écrit avec la première négation modifiée.

∃x∀y((y ∈ x) ⇔~ (y ∈ y)) .

Si cet ensemble existe nous pouvons introduire un lettre notée: a, compte tenu de son unicité (axiome d'extensionalité). Cette énoncé devient

∀y((y ∈ a) ⇔~ (y ∈ y)) .

et il implique que nous devions instancier les occurrences de y par la lettre a du fait du kanteur universel

((a ∈ a) ⇔~ (a ∈ a)) .

Or, la nouveauté vient du fait que cette expression s'écrit dans cette logique

car nous disposons de la thèse de la logique de la coordination modifiée (Calcul des propositions modifiée) qui veut que

(⇔(p ⇔~ p))

et qu'il suffit d'écrire à l'occasion de la proposition (a ∈ a) .

Nous obtenons ainsi un premier résultat dont nous allons nous servir par la suite :

L'ensemble des x vérifiant la relation ~ (x ∈ x) écrite avec la première négation modifiée, est lui même un ensemble vérifiant la relation () écrite avec la seconde négation modifiée.

                                           fin page 9, suite page 10 à droite ci-contre ..............>

suite page 10, ci-dessous,

II. 1.
Situation de l'obstruction qui s'oppose à
ce que la classe de Russell soit un ensemble

     Si nous voulons construire dans cette logique l'ensemble des éléments qui vérifient la négation de l'auto appartenance ~ (x ∈ x) soit l'énoncé qui le caractérise

∃x∀y((y ∈ x) ⇔~ (y ∈ y))

nous pouvons partir de la thèse logique qui se propose comme

.

     Il s'agit de préciser le lieu de l'impossibilité de la construction, en tant qu'ensemble, de la classe des ensembles qui ne s'appartiennent pas à eux mêmes

     Cet énoncé est par définition du premier kanteur l'abréviation de la formule

¬∃x( (x) ∧ )

il écrit qu'il n'existe pas dans l'aire de la classe d'ensembles qui satisfassent la condition imposée aux objets tels que celui que nous recherchons.
      Il s'agit d'une thèse logique de la topologie du sujet. Démontrons ce fait.

     Il suffit de revenir à la définition et à une propriété de la seconde négation modifiée, elle est définie par l'énoncé

(¬P(x) ∧¬ ~ P(x))

et donne lieu à la propriété logique caractéristique

(⇔ ( (x)∧¬P(x))) .

     Ainsi notre expression devient

¬∃x( (x) ∧ ( (x)∧¬(x ∈ x)))

qui est une thèse du fait de l'exclusion mutuelle de la logique classique,

(x) ¬(x) .

     En effet, la négation en logique classique nous impose,

∀x(P(x) ∨¬P(x)) soit ¬∃x(P(x) ∧¬P(x)) .

     Pour conclure cette étape, reconnaissons que la première formule du côté femmes

comme nous venons de l'expliciter, nous impose, si nous reprenons ce que nous avons précisé à l'étape précédente, une lecture de cette formule et de sa conséquence dans la recherche de notre objet.
     Puisqu'il n'existe pas d'élément du côté du sujet /S(x) satisfaisant la seconde négation de la relation d'appartenance alors

¬∃x((x) ∧∀y((y ∈ x) ⇔~ (y ∈ y)))

il ne peut pas exister un objet qui serait l'ensemble de ceux qui vérifient la première négation de cette relation  ~ (y ∈ y)) comme dans la situation classique dont le sujet barré représente le lieu du plongement de la logique d'Aristote. Ce sujet est divisé par le prédicat en deux moitiés et seulement deux moitiés symétriques, de manière stricte.

Fin de la page 10,

II. 2.
Construction, dans l'Autre du sujet
d'un modèle d'hors univers de cette classe
x(x ∈ x)

                                                                                                                                ...p11,
Constructibilité axiomatique et analytique de l'objet en topologie du sujet.
     Mais nous pouvons construire dans cette logique l'ensemble des éléments qui vérifient la négation de l'auto appartenance ~ (x ∈ x) soit l'énoncé qui le caractérise

∃x∀y((y ∈ x) ⇔~ (y ∈ y))

si nous adoptons l'axiome logique qui se propose à nous comme seconde formule de la sexuation de ce côté dit des femmes

x(x ∈ x) .

     Cet axiome n'est pas une thèse.

    Construisons, dans l'Autre du sujet, hors univers alors, un modèle de cette classe des ensembles qui ne s'appartiennent pas à eux mêmes dans l'univers classique comme un ensemble qui existe mais est dit : "pas tout", de ce fait.

     La seconde formule, notre axiome de ce côté s'explicite ainsi

¬∀x( (x) ⇒ (x ∈ x))

ce qui par dualité classique des kanteurs nous assure d'une existence

∃x( (x) ∧¬P(x))

correspondant, du fait de sa propriété signalée à l'étape précédente, à la seconde négation modifiée ici de l'auto appartenance. Cet axiome écrit,

∃x .

     Ainsi si il existe de tels objet et que la thèse logique, le première formule côté femmes, impose qu'ils ne soient pas dans le sujet, ils suffit de conclure : ils sont hors du sujet.
Nous pouvions nous en douter par ailleurs si nous lisons bien la propriété de cette seconde négation. Elle situe les objets dans l'Autre du sujet.

     A partir d'ici rien n'objecte en logique, pour des raison analytique, à leurs existence, écrite ici

∃x( (x) ∧∀y((y ∈ x) ⇔~ (y ∈ y)) ,

mais il reste à s'assurer que leur existence n'est pas contredite par des raisons synthétiques, en mathématiques par exemple.

     Nous passons à la seconde étape du commentaire de la seconde formule pour voir si rien n'objecte en mathématique à sa conséquence dans notre quête d'un objet femme qui puisse se dire pas toute contrairement à la mère : cette folle avec son désir insatisfait, symptôme pour l'Homme.

Fin de la page 11.

Constructibilité synthétique de l'objet en mathématique.     .....................................p12

       Nous pouvons donner un diagramme, de la facture de Euler qui va nous permettre de raisonner sur un modèle géométrique avec le type de formules inventées par Frege et Peirce, avant de résoudre la situation de manière plus algébrique par un calcul directe.
     Il s'agit du schéma de l'énoncé ∀y ((y∈a) ⇔ ~(y∈y)) présent à un moment dans l'ensemble de nos déductions.

∀y( (y∈a) ⇔ ( (y) ∧ (yy)) )  ........ diagramme ci-contre ....>

Nous avons vu que l'objet a ne peut pas être construit dans les zones non vides de (y) notées (1) et (2) dans ce diagramme.).

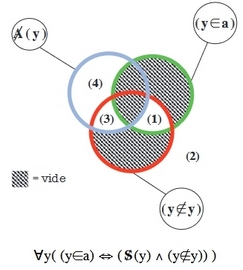
     Car la première formule implique qu'il ne peut être construit dans ces deux zones,

⇒ ¬∃x((x) ∧∀y((y ∈ x) ⇔~ (y ∈ y))) .

    Ainsi l'antilogie [ (a∈a) ⇔ (aa) ] s'impose comme nécessaire dans(y) et dans notre diagramme quatre zones correspondent maintenant à la valeur faux de manière toute aussi nécessaire et se vident, s'ajoutant au zones où l'objet, du fait de notre kantification universelle précédente, ne peux pas se trouver parce qu'elles sont vides également par définition de l'objet cherché.

                                                                suite de la page 12, à droite : Un mot d'esprit .....>

Proposons à ceux que cela importe donc, de reprendre la présentation diagrammatique, avec notre modèle de la situation qui s'écrit !∀y ( (y∈a) ⇔ ~ (y∈y) à repartir ici de la formule

[ (x) ∧∀y( (y ∈a) ⇔~ (y ∈ y) )].

Dans notre figure précédente, dans ce nouveau cas de formule passant de (y) à (y),
l'objet a doit se trouver dans un lieu dont les zones notées : (3) et (4), dans notre diagramme nous donnent une première approximation.

Si nous le trouvions là, cette formule devient

[(a) ∧ ( (a∈a) ⇔ ~ (a∈a) )]

car

∀y ( (y∈a) ⇔ ~ (y∈y) )

doit pouvoir supporter l'instanciation

( ( (a∈a) ⇔ ~ (a∈a) )

du fait du kanteur universel qui l'ouvre, soit comme nous l'avons précisé plus haut

qui devient constructible grâce à notre axiome,

x (x ∈ x)

la seconde formule de la sexuation du côté des femmes.

Or cette dernière formule correspond à un nouveau diagramme à la manière de Euler et de Venn.

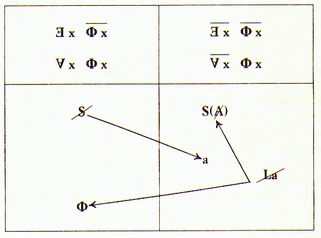
                                                  diagramme ci-contre, Haut droite, ....>

Donnons le accompagné d'un autre diagramme qui va nous éclairer.
Le lecteur, même débutant, peut se reporter aux diagrammes et aux formules de l'équivalence matérielle et de sa négation, la différence symétrique, de la coordination classique des concepts comme des propositions que nous reproduisons ici. .........................ci-contre, ...>

En effet, l'instanciation de y par la lettre a produit un mot d'esprit littérale et graphique du fait d'une identification des prédicats monadiques distincts qui ne sont ...

fin de la page 13,

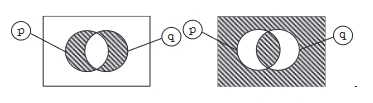
... pas de simple négations mutuelles (y∈a) et (yy), donnant lieu à des propositions (a∈a) et (aa) qui deviennent entre elles des négations mutuelles au sens strict leur non équivalence

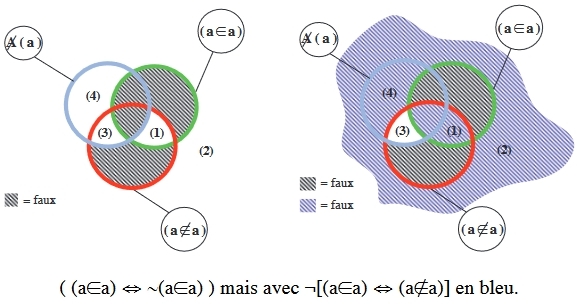
¬[(a∈a) ⇔ (aa)]

vide une partie du diagramme.✔

     Ainsi l'antilogie [(a∈a) ⇔ (a a)] s'impose comme nécessaire et dans notre diagramme quatre zones correspondent maintenant à la valeur faux de manière toute aussi nécessaire et se vident, s'ajoutant au zones où l'objet, du fait de notre kantification universelle précédente dans sa définition, ne peux pas se trouver parce qu'elles sont vides également.

Or, malgré ce vidage intempestif, cet évidemment qui pourrait produire ce que certains veulent croire de l'évidence de leurs préjugés, ce vide pourtant, contrairement au cas de l'échec précédant situé dans (y) où notre formule devenait globalement une antilogie, n'objecte pas à ce reste, ici une zone, notée : (3), qui reste indéterminée, la formule n'est pas inconsistante et permet d'y trouver l'objet a, à sa place et en son lieu d'ex-sistence originale pour la logique impensée des sciences des hommes. Hors univers est acceptable pour l'écriture logique.

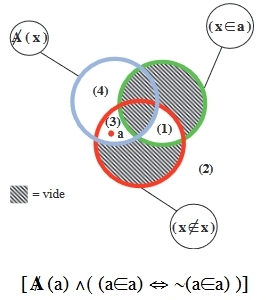
                               lire le schéma ci-contre .....................................>
                                               [(a) ∧ ( (a∈a) ⇔ ~ (a∈a) )]

     Notre formule alors, n'est pas une antilogie globale et fausse par nécessité comme toute antilogie qui doit être rejetée, elle tolère de voir l'objet situé dans cette zone (3) correspondant à la formule qui résume la situation

[ (a) ∧ ¬ (a∈a)]

Ceci nous permet d'adopter dans notre topologie, comme axiome ou comme thèse déductible sans risque d'inconsistance, l'énoncé

∃x [ (x) ∧ ∀y ( (y∈x) ⇔ ~ (y∈y) )]

qui produit cet objet a qui ex-siste dans ces conditions hors de (x) dans son Autre qui est barré (x) = ¬ (x). Cet objet nous assure de l'ex-sistence dans qui s'écrit

(2.0) ∃x [ (x) ∧ ¬ (x∈x)].

et se lit dans le dernier diagramme.

     Sans risque d'inconsistance disons nous, cette précision signale au contraire que c'est bien à partir d'ici que se présente l'ouverture de l'étude des conditions qui vont trivialiser cette situation ou de ses conséquences de trivialisation. Elles ne sont pas quelconques, indifférentes, obligées, imposées de n'importe quelles manières.............................(fin dela page 14)

avant que de se produire pour confirmer que ce lieu n'est pas tenable en faits, mais de quels faits s'agit-il : ceux qui se produisent au lit, dans la rue, au gouvernement ?
     Franchissons alors, ici encore une fois, la dernière étape, pour retrouver notre propos, avec la seconde formule de la sexuation côté femme. Cet ultime énoncé noté : (2.0), s'écrit de façon très classique avec un kanteur universel,

(2.1) ¬∀x [ (x) ⇒ (x∈x)]

et comme énoncé réduit toujours très classiquement, malgré la lettre qui condense
la modification topologique de la logique,

(2.1) ¬∀ x (x∈x)

     Ici aussi, nous retrouvons la définition que nous proposons du second kanteur original introduit par Lacan à cette occasion,

(2.2) x (x∈x)

devant notre prédicat (x∈x) non nié cette fois comme nous l'avons déjà fait remarquer plus haut

Conséquence pour la lecture des formules du côté femme.
     Notre construction trouve ainsi, en définitive, parce que de manière redoublée, c'est à dire fondée, sa fonction dans le discours analytique. En effet l'expression de cette axiome correspond trait pour trait à l'autre formule de la sexuation côté femmes qui asserte : " les femmes ne sont pas toutes... "

x Φ(x)

ce qui signifie bien, avec ce kanteur, un mode d'existence, lisible dans notre dernier diagramme avec (x∈x) en place de Φ(x) du côté des femmes, ex-sistence qui n'est pas inscriptible en logique classique selon Aristote.

      Lacan reprenant ainsi le sens selon Aristote (Écrits volume 2 p.465),
           "Ce n'est pas là le sens du dire qui s'inscrit de ces kanteurs. "
ajoute
           "Il est : que pour s'introduire comme moitié à dire des femmes, le sujet se détermine de              ce que, n'existant pas de suspens à la fonction phallique..."

ce que nous construisons dans la première formule :

avec (x∈x) en place de Φ(x),

           "... tout puisse ici s'en dire, même à provenir du sans raison. Mais c'est un tout... "

c'est un ensemble dans (x) d'après ∃x [ (x) ∧ ¬ (x∈x)] qui s'écrit ∃x et que
nous avons montrer suivre de notre axiome

x (x ∈ x) ¬∀x ( (x) ⇒ (x ∈ x))

¬∀x ((x) ⇒ (x ∈ x)) ⇔ ∃x ( (x) ∧¬ (x ∈ x))

établit bien que c'est un tout...

           "...d'hors univers... "

car (x) = ¬ (x), où(x) est le plongement dans la topologie du sujet, de l'univers de la science, interprétée de façon classique par la raison scientifique alors que notre objet est un tout dans (x)...

"... lequel se lit tout de go du second kanteur comme pas tout"

x (x∈x).

" Dans (x) ils ne sont pas tous, à s'appartenir à eux même.", où il s'agit bien, dans ce kanteur pastout, d'une ex-sistence puisqu'il est ordinaire de noter que dans un énoncé universel c'est d'une non existence qu'il s'agit et, par conséquent, avec la négation d'un énoncé universel c'est bien d'une existence dont il s'agit.

Mais si on nous a bien lu, au travers de cette topologie et des définitions qu'elles proposent nous pouvons tenir chacun de ces énoncés à condition de les labéliser par un caractère d'assertion indexé par nos constantes logiques respectives et .

                Introduisons des caractères d'assertion dépendant du lieu où ça se thomme

¬x (x∈x).
Nous pouvons expliciter ces expressions grâce à leurs définitions respectives
: (⇒ ).
¬x (x∈x) : ( ⇒ ¬ x(x∈x)) : ( x (x∈x) ⇒ ).

Force est alors de constater la relation qu'elles entretiennent entre elles du fait
de,

elle est assez élémentaire et de conclure par la thèse

tenable même en topologie du sujet seul lieu où elle est inscriptible comme cela se vérifie de n'importe quel prédicat P(x).

......................................................suite page 16 à droite, .......>

 page 16, suite et fin,

Qu'elles ne soient "pas toute" à tomber sous le prédicat phallique implique :
" il n'y en a pas " qui dise non à la fonction phallique.
     Ici écrite, une ex-sistence, du fait de la modification introduit l'hors univers et l'impose, comme fait, de son écriture réglée : son savoir écrit sur du papier à musique, qui se cherche d'ordinaire dans les symptômes ou les sinthomes comme on voudra, passant à la lettre dans la vérité, réduisant la jouissance qu'elle traverse à une ligne (bande de Moebius), quoi qu'elle en dise.
Nous ne lui demandons plus son avis, ni même si c'est de son goût. Ici la vérité subit, en une joyeuse involution, le savoir en échec, malgré la Loi, sur l'échelle renversée, - queue par dessus tête, n'ayant plus ni cul ni tête -, dans l'instant du désir.✔

Jean Michel Vappereau
de Buenos Aires, mayo 2009
à Paris, le 9 Juin 2007